Bonds Away
Historical Look at Stock/Bond Risk-Return in Varying Valuation Environments
A few weeks ago, I published To Bond or Not To Bond. This post provides a historical perspective on the give and take of risk and return vs stock and bond valuations.
The Efficient Frontier
This is just a little background for anyone that is unfamiliar with the risk-reward tradeoff discussed below. Feel free to jump ahead if you’ve seen and understand the chart below.
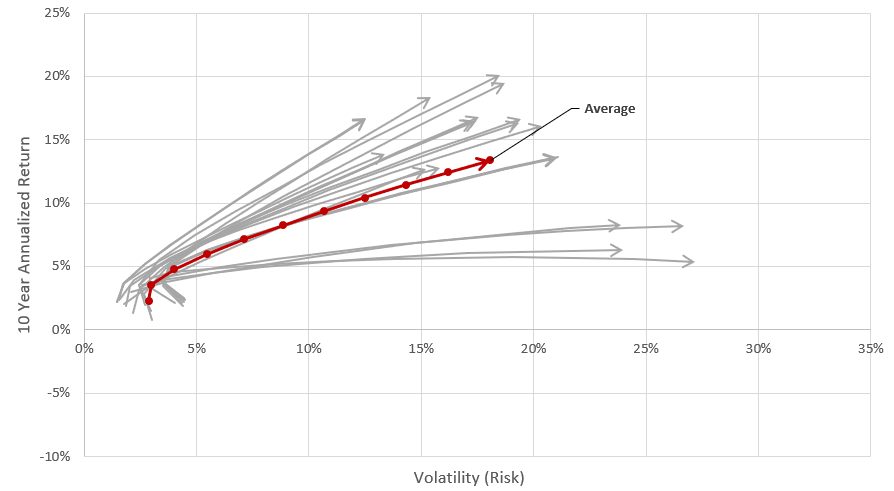
For investing, there is generally a trade-off between risk and return. The more risk you’re willing to take, the more exposure you have to potential returns. For a portfolio of stocks and bonds, we can view that trade-off as follows.
The image above gives the return vs volatility (measured by standard deviation) for different portfolio weightings of stocks (S&P 500) and bonds (10 year treasuries). These portfolios are rebalanced at the end of each year. The data presented is averaged for all years from 1928 to 2010.
The primary observations are:
As you weight more towards stocks, the average return (vertical axis) increases.
As you weight more towards stocks, your average risk (horizontal axis) also increases.
You may also notice that the plot curves inward around the (10/90 mark). This is actually a quite profound observation of diversification; we see that going from 100% bonds to 90% bonds / 10% stocks will actually reduce risk while increasing return. This is known as the “free lunch” that diversification offers.
But, the primary takeaway is that, on average, increasing exposure to stocks increases both risk and return.
The key phrase is “on average”. I want to explore the relation of relative valuations for stocks and bonds as I looked at in my last post: “To Bond or Not To Bond”
Bringing Back The Equity-Bond Spread
From my last post, we defined the equity-bond spread as follows:
Equity-Bond Spread = (1/CAPE) - (10 Year Treasury Yield)
This can be used as a proxy for how attractive (or unattractive) equities look compared to bonds. In this post we’ll look at how this spread affects the risk-return profile of stocks and bonds.
A Tale of Two Halves
There are 83 years in our data set (between 1928 to 2010). A great place to start looking into this data is to split our data set at the median equity-bond spread, which is a spread of 0.7%. So let’s recreate our risk-return chart, now plotting the data above and below the median separately.
Note that a spread above the median (blue curve) intuitively represents stocks being relatively attractive compared with bonds. Inversely, a spread below the median (orange curve) corresponds to stocks being less attractive.
First, it’s important to point out that we shouldn’t look at absolute returns in this plot. We don’t normalize for starting yields in any way, so it’s not appropriate to assume, just from this chart, that a large spread will result in greater absolute returns than small or negative spreads. In fact, the average CAPE ratios are 21.2 and 13.9 for the orange and blue curves, respectively. So it’s no wonder absolute returns might be higher for the blue curve.
The main observation from this chart is that the orange curve is quite flat, while the blue curve is much more steep. Looking at the orange curve (narrow and negative spreads), we see that the trade-off on risk reward look much less enticing. For instance, going from a 90/10 portfolio to a 100/0 portfolio adds a full percent of additional volatility, but only 0.03% of additional return. In fact, going from a 60/40 portfolio to an all stock portfolio adds only 0.4% in annualized return, but increases volatility by almost 50%.
We can see this, further by plotting the slope of the curves. This presents the risk-reward trade-off as a numerical value as defined by the change in return divided by the change in volatility. Figure 3 shows the slope of the curves in Figure 2. A low value below corresponds with incurring a lot of extra risk for very little extra return.
This is in line with what we saw in “To Bond or Not To Bond”; that narrow and negative spreads may lead to muted excess returns of stock-heavy portfolios.
Sample Set Caveat
There is a big caveat hidden in this data, however. The sample set is quite bifurcated, where most of the high spread years were in the early 20th century, while the low spread era occurred mostly post 1980. See the plot below.
If we can convince ourselves that the mechanics of market behavior has changed since the early / mid 20th century, then this data may not offer much insight.
I think it’s worth digging a little deeper…
Diving Deeper
Because the median split was so bifurcated, I wanted to see if dividing the data further offered any more insight. The data presented below is for the same sample set, now divided into quartiles.
First let’s look at the frequency chart.
We can see that the distribution is a little more dispersed, but the first quartile is still primarily dominated by the post 1980 time period and the fourth quartile is still dominated by the 1930’s to 1950’s.
After performing the same exercise from the Tale of Two Halves, Figure 6 shows the risk return portfolio plots for each of the quartiles. Again, take note of the curve slopes (and general shapes) rather than absolute values. We see that the payoff for additional risk increases as we progress through each spread quartile. This still tracks our two quantile observations.
Data Dump
Diving even deeper, we can plot out the risk-return charts for each individual year in our set. Figures 7 thru 10 show this for each quartile. This is meant to highlight that the efficient frontier curves are just an average, and that there’s a wide range of possible outcomes. Just because, on average, we might (or might not) expect large excess returns, doesn’t mean that it’ll actually come to fruition. I’ll add some lite commentary as we go.
Fun fact: The lines sloping up in Figure 7 are the time periods that capture the runup into the dotcom bubble (starting years: 1985 to 1992). The lines sloping down are mostly (you guessed it) the periods starting just before the dot com bubble bursts (starting years: 1998 to 2002).
The long downward sloping line in Figure 8 is 1929 (start of the great depression). The long downward sloping lines in Figure 9 also correspond to the periods leading into the great depression.
The fourth quartile (years with the widest positive equity-bond spread) definitely looks like it produces the most consistent returns per unit of risk. But again, this was largely buoyed by the post-war bull markets in the 1940’s and 50’s.
One additional note, the bottoms of the GFC in 2009 and the Covid Crash in mid March of 2020 were both firmly in this quantile. We all know how the ten years following 2009 have faired and, so far, March of 2020 looks to have been a great time to have gone stock heavy as well.
Where Are We Today?
Today, we sit firmly in the first quartile (worst spread quantile in history) with an equity-bond spread currently at -1.5%. This means that, on average, we can probably expect muted excess returns: i.e., a 60/40 portfolio may perform only slightly worse than a 100/0 (all stock) portfolio while providing investors with a much smoother ride. But as we’ve also discovered, the distribution of possibilities is incredibly wide, and can depend greatly on where we stand in the business, credit, and market sentiment cycles.